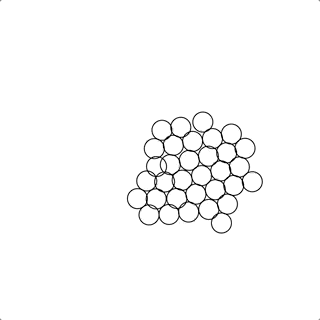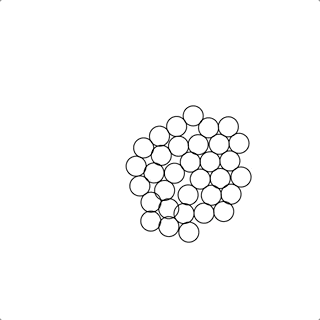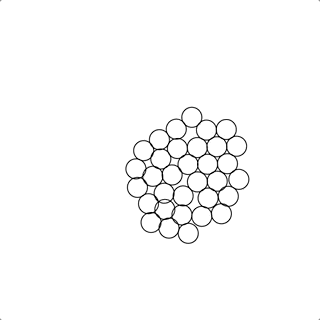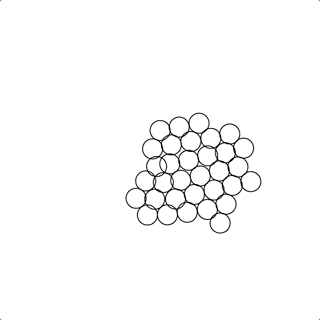
本期知识点密度:★★★✩✩
本期要做的事:
做出吸引和排斥共存的效果
如果觉得太长太麻烦
可以直接移步【太长不看版】
本期主要内容:
- 一:Processing中的向量(PVector)
- 二:求解物体之间的排斥
- 三:同时施加吸引与排斥
Processing中的向量(PVector)
向量(Vector)是制作动态图形必不可少的工具之一
它可以方便的表示物体的位置、速度、加速度等状态,也可以求解物体之间的空间关系;
Processing为我们提供了原生的向量数据类型:PVector
这样的话,我们就可以使用PVector内置的函数来方便的实现物体间力的施加。
下面是一个简单的使用向量的例子:1
2
3
4
5
6
7
8
9
10
11PVector v1, v2;
void setup() {
v1 = new PVector(40, 20);
v2 = new PVector(25, 50);
line(0, 0, v1.x, v1.y);
line(0, 0, v2.x, v2.y);
v2.add(v1);
line(0, 0, v2.x, v2.y);
}
这段代码定义了两个不同的向量,并分别将他们绘制;
之后再将两个向量相加,绘制出相加后的向量;
向量的更多具体用法,大家可以查看File——Examples——Topics——Vectors里的几个例子:
求解物体之间的排斥
对于求解排斥的问题,最容易产生关联的的就是求解“流体”之间的作用力,在计算机图形学界,求解流体有两大方向,分为欧式方法(Eulerial Methods)和拉式方法(Lagrangian Methods),在拉式方法中,流体是由粒子的集合所刻画,其中最为常用的是 SPH(Smoothed Particle Hydrodynamics) 平滑粒子动力学 和它的一些改进算法 这个方法的确可以很好的求解由粒子刻画的的无边界流体的运动状态;
这个方法的确可以很好的求解由粒子刻画的的无边界流体的运动状态;
然而
我们是一个新手向的入门级教程
教SPH太反人类了
所以我们接下来会用最简单的向量操作
借用拉格朗日方法的思想
来初步模拟粒子排斥的问题: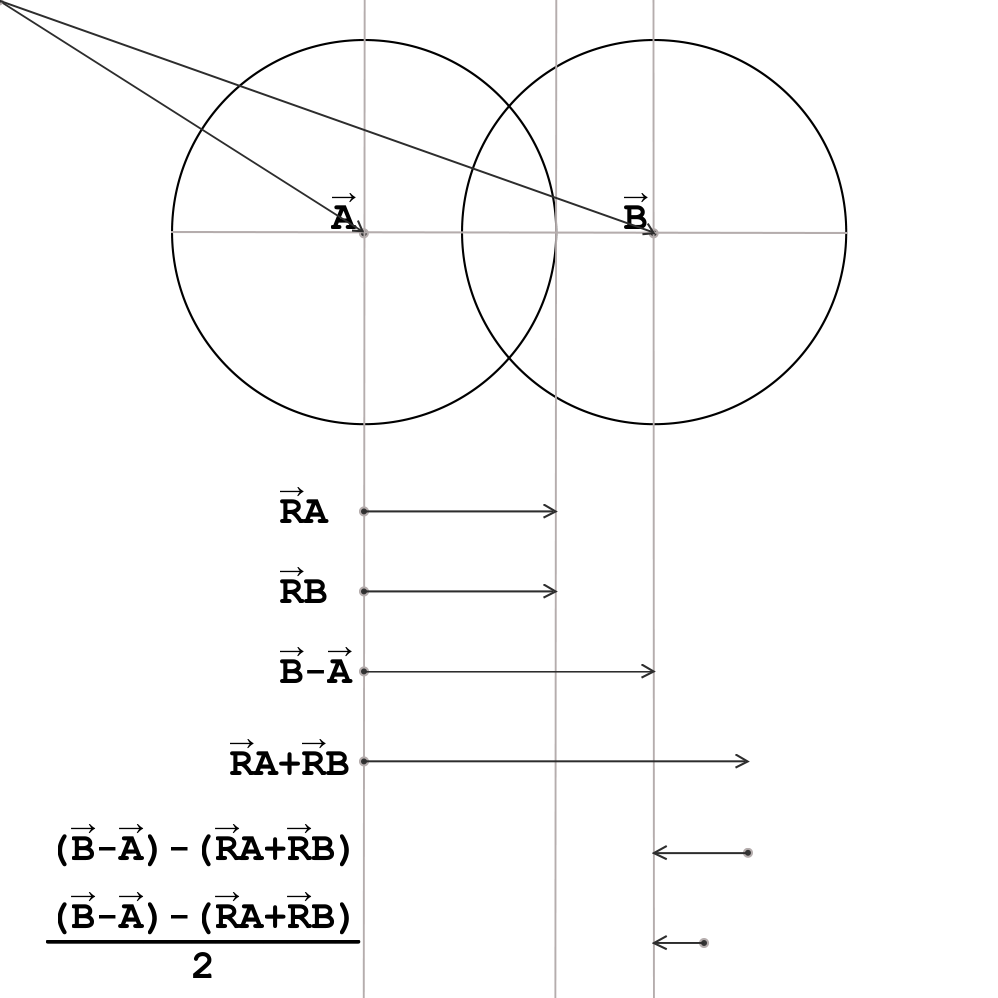
假设有两个粒子:A、B
他们的位置为 \(\vec A\)、\(\vec B\),半径分别为 \(\vec RA\)、\(\vec RB\)
那么,两个粒子的间距用向量表示为 \(\vec B- \vec A\),两个粒子的半径之和为 \(\vec RA + \vec RB\)
根据示意图,两个半径相加相当于把 重叠部分计算了两次,所以可以用半径之和减去间距,计算出重叠部分的向量。
也就是:\((\vec B - \vec A) - (\vec RA + \vec RB)\)
求出了粒子碰撞后重叠部分的距离之后
接下来需要根据重叠的程度来施加排斥
因为两个粒子只需要移动重叠部分一半的距离即可分离开
那么实际(给A粒子)施加的排斥向量是:\(\frac{(\vec B - \vec A) - (\vec RA + \vec RB)}{2}\)
同理,给B粒子施加相反的向量即可:\(-\frac{(\vec B - \vec A) - (\vec RA + \vec RB)}{2}\)
用代码表示为:1
2
3
4
5
6
7
8
9
10void repel(PVector A, PVector B) {
PVector BsubA = PVector.sub(B, A); //向量B-A
PVector RAaddRB = BsubA.copy(); //由于粒子每次碰撞的方向不同,所以半径向量需要根据碰撞方向来确定,故复制了向量B-A
RAaddRB.normalize(); //归一化RA+RB向量
RAaddRB.mult(Radians*2); //将RA+RB扩大到两个半径之和
PVector RepelA = PVector.sub(BsubA, RAaddRB);//计算重叠部分的向量
RepelA.mult(0.5); //重叠部分减半
A.add(RepelA); //对A粒子施加排斥
B.add(RepelA.mult(-1)); //对B粒子施加排斥
}
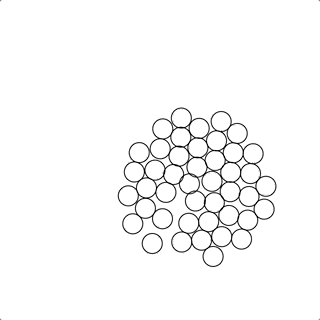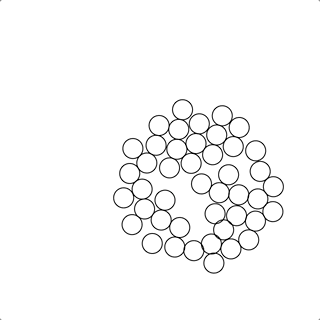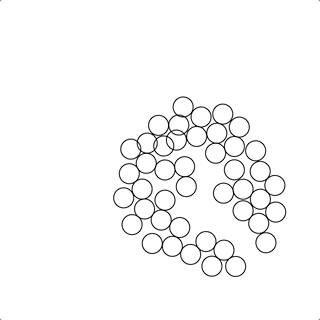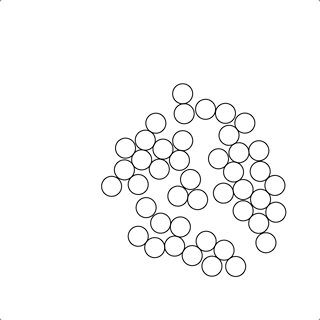
完整代码为:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42float Radians = 10;
ArrayList<PVector> points = new ArrayList<PVector>();
PVector mouse;
void setup() {
size(500, 500, FX2D);
noFill();
points.add(PVector.random2D());
}
void draw() {
background(255);
mouse = new PVector(mouseX, mouseY);
points.get(0).x = mouseX;
points.get(0).y = mouseY;
if (mousePressed) {
mouse.add(PVector.random2D());
points.add(mouse);
}
for (int i=0; i<points.size(); i++) {
for (int j=0; j<points.size(); j++) {
if (i!=j && PVector.dist(points.get(i), points.get(j)) <= Radians*2) {
repel(points.get(i), points.get(j));
}
}
}
for (PVector p : points) {
PVector relative = PVector.sub(mouse, p);
relative.normalize();
p.add(relative);
ellipse(p.x, p.y, Radians*2, Radians*2);
}
}
void repel(PVector A, PVector B) {
PVector BsubA = PVector.sub(B, A);
PVector RAaddRB = BsubA.copy();
RAaddRB.normalize();
RAaddRB.mult(Radians*2);
PVector RepelA = PVector.sub(BsubA, RAaddRB);
RepelA.mult(0.5);
A.add(RepelA);
B.add(RepelA.mult(-1));
}