【第四期】矩形的旋转相切

发表于 | 更新于

本期知识点密度：★★✩✩✩

大家嚎！我又回来啦~
我们先解答本期的问题：如何实现精确的旋转矩形相切
就像这样：

问题剖析：

想在大方块内绘制一个稍微小一点的方块，需要知道它的旋转角度和边长

旋转角度直截了当，只需使用rotate()函数每次旋转一个固定值即可，就像这样：

1
2
3
4
5
6
7
8
9
10
11
12
13
void setup() {
  float l=300;
  size(500, 500);
  rectMode(CENTER);

  translate(width/2, height/2); //将画布原点移动到屏幕中央
  while (l>5)               //当边长大于5像素
  {
    rotate(15*DEG_TO_RAD);  //每次旋转15度
    rect(0, 0, l, l);       //绘制方形
    l-=5;                   //方形边长每次减小5像素
  }
}

这段代码能很好的处理旋转和绘制，但并没有把角度和正方形边长的变化联系起来，我们接下来就要关联这两个变量。

首先，如果有内外两个相切的正方形，我们可以假设，大小正方形的边长分别为L和l，如图：
接下来，可以将图中的 α 角视为旋转角，可得到 α 角的对边长\(l×sinα\) 和邻边长\(l×cosα\)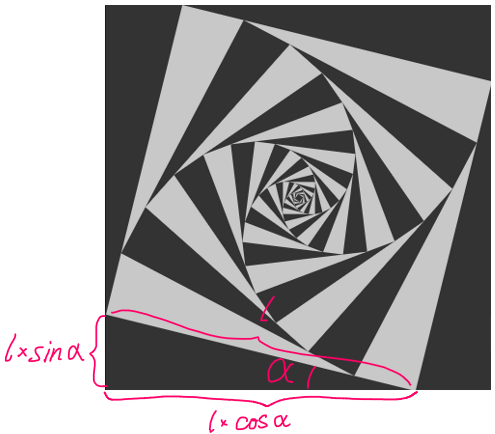
同时，另一组边的关系也可以轻易得出：$$L=(L-a)+a$$ 其中 $$(L-a)=l×cosα$$ $$a = l×sinα$$
那么，在得知角α的大小后，我们可以列出如下等式：$$L=l×cosα+l×sinα$$ 经变换后得到：$$L=l×(sinα+cosα)$$ $$l=\frac{L}{sinα+cosα}$$

1
2
3
4
5
6
7
8
9
10
11
12
13
void setup() {
  float l = 500;
  float rotation = 15*DEG_TO_RAD;
  size(500, 500);
  rectMode(CENTER);

  translate(width/2, height/2);
  while (l>5) {
    rect(0, 0, l, l);
    rotate(rotation);
    l = l / (sin(rotation)+cos(rotation));
  }
}

稍加修饰

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void setup() {
  float l = 500;
  float rotation = 15*DEG_TO_RAD;
  int count = 0;
  size(500, 500);
  noStroke();
  rectMode(CENTER);

  translate(width/2, height/2);
  while (l>5) {
    if (count%2==0)  fill(51);
    else fill(200);
    rect(0, 0, l, l);
    rotate(rotation);
    l = l / (sin(rotation)+cos(rotation));
    count ++;
  }
}

下期预告：

一：如何实现Processing启动界面的渐变线条
二：如何复刻完整的启动界面