【第三期】圆与方块的接触

发表于 | 更新于

本期知识点密度：★★★✩✩

点和圆的接触

初中数学曾经学过：圆的判定公式

$$x^2+y^2=r^2$$

所以想要求解一点是否在圆内，只需判断 \(x^2+y^2\) 和 \(r^2\) 的关系即可；

前者大于后者，则意味着点在圆外

前者小于后者，则意味着点在圆内

前者等于后者，则意味着点在圆上

同时为了消除圆本身的位置偏移，需要减去圆心的偏移量（a，b）

$$(x-a)^2+(y-b)^2=r^2$$

程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
float a=200, b=200, x, y;

void setup() {
  size(400, 400);
}

void draw() {
  background(100);
  x = mouseX;
  y = mouseY;

  ellipse(a, b, 120, 120);

  if (sq(x - a) + sq(y - b) <= sq(60))
    fill(255, 0, 0);
  else 
    fill(255);
}

圆和圆的接触

圆与圆的接触也很简单，只需要检测两个圆心点的距离是否小于半径之和即可

原理和上面的实质是相同的：即检测（A圆心——B圆心）两点间的距离

$$(Xa-Xb)^2+(Ya-Yb)^2=(Ra+Rb)^2$$

（其中 Xa Ya 代表圆A的坐标，Xb Yb 代表圆B的坐标，Ra Rb 代表两圆的半径）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
PVector Ca = new PVector(100, 100);  //圆 A
PVector Cb = new PVector(200, 200);  //圆 B

void setup() {
  size(400, 400);
}

void draw() {
  background(0);
  Ca = new PVector(mouseX, mouseY);
  
  ellipse(Ca.x, Ca.y, 120, 120);
  ellipse(Cb.x, Cb.y, 80, 80);

  if (sq(Ca.x - Cb.x) + sq(Ca.y - Cb.y) <= sq(60+40))
    fill(255, 0, 0);
  else 
    fill(255);
}

或者直接使用Processing计算距离的函数dist()

1
if (PVector.dist(Ca, Cb) <= 60+40)

圆和方块的接触

圆和方块的接触
只需将上面的方法稍作扩展即可

计算距离的两点，从（圆心——圆心），变成了（圆心——方块上离圆心最近的点）

这时，问题转化成了：
如何计算出方块上距圆心最近的点？


我们先规定：以方块左上角为坐标点，然后只考虑X方向，假设出不同条件：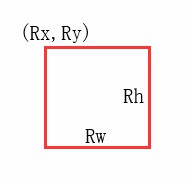

—— 以下是只考虑 X方向 时的三种条件：——

条件一：

方块顶点在圆心点右侧：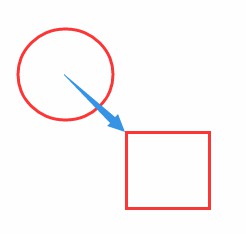


可以看出，方块距圆心最近的X，是顶点：Rx

条件二：

方块顶点已经到了圆心另一侧，但其他部分还没有完全移动到另一侧：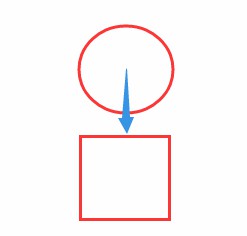


可以看出，方块距圆心最近的X，是圆心：Cx

条件三：

整个方块已经完全移动到了圆心另一侧：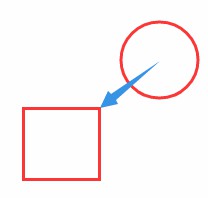


可以看出，方块距圆心最近的X，是方块顶点+方块宽度：Rx+Rw

这样一来，就可以写出X方向上，方块距离圆心最近距离的计算公式：

$$Px = max(Rx,min(Rx+Rw, Cx))$$

用程序表达起来也很简单：

1
2
3
4
5
6
7
8
9
if(Rx > Cx){            //条件一
    Px = Rx;
}
else if(Rx+Rw > Cx){    //条件二
    Px = Cx;
}
else if(Rx+Rw < Cx){    //条件三
    Px = Rx+Rw;
}

同理，Y方向上一样能写出：

$$Py = max(Ry,min(Ry+Rh, Cy))$$

1
2
3
4
5
6
7
8
9
if(Ry > Cy){            //条件一
    Py = Ry;
}
else if(Ry+Rh > Cy){    //条件二
    Py = Cy;
}
else if(Ry+Rh < Cy){    //条件三
    Py = Ry+Rh;
}

得到Px和Py后，我们就回到了最原始的方法：

$$(Cx-Px)^2+(Cy-Py)^2=Cr^2$$

为了避免if语句表达起来太累赘，可以直接使用min() max()函数来表示公式：

1
2
Px = max(Rx, min(Rx+Rw, Cx));
Py = max(Ry, min(Ry+Rh, Cy));

最终程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
float Cx, Cy;
float Px, Py;
float Rx=150, Ry=150, Rw=100, Rh=100;

void setup() {
  size(400, 400);
}

void draw() {
  background(0);

  Cx = mouseX;
  Cy = mouseY;
  ellipse(Cx, Cy, 100, 100);
  rect(Rx, Ry, Rw, Rh);

  Px = max(Rx, min(Rx+Rw, Cx));
  Py = max(Ry, min(Ry+Rh, Cy));

  if (sq(Cx - Px) + sq(Cy - Py) <= sq(50))
    fill(255, 0, 0);
  else 
    fill(255);
}

本期引用：

https://yal.cc/rectangle-circle-intersection-test/