为什么要重复造轮子
直接用库才对嘛
- 下载Toxi库
- 复制以下代码
- 完成

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35import toxi.geom.*;
import toxi.physics2d.*;
import toxi.physics2d.behaviors.*;
VerletPhysics2D physics;
AttractionBehavior2D mouseAttractor;
Vec2D mouse;
void setup() {
size(500, 500, FX2D);
noFill();
physics = new VerletPhysics2D();
physics.setDrag(0.30f);
addParticle();
mouse = new Vec2D(mouseX, mouseY);
mouseAttractor = new AttractionBehavior2D(mouse, 500, 0.2);
physics.addBehavior(mouseAttractor);
}
void draw() {
background(255);
mouse.set(mouseX, mouseY);
physics.particles.get(0).x = mouseX;
physics.particles.get(0).y = mouseY;
if (mousePressed) {
addParticle();
}
physics.update();
for (VerletParticle2D p : physics.particles) {
ellipse(p.x, p.y, 20, 20);
}
}
void addParticle() {
VerletParticle2D p = new VerletParticle2D(Vec2D.randomVector().scale(5).addSelf(mouseX, mouseY));
physics.addParticle(p);
physics.addBehavior(new AttractionBehavior2D(p, 20, -1.2f, 0.01f));
}

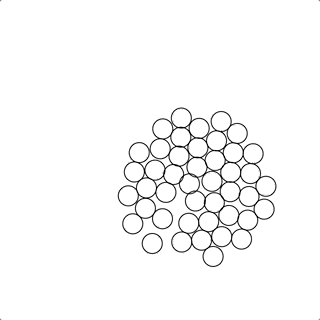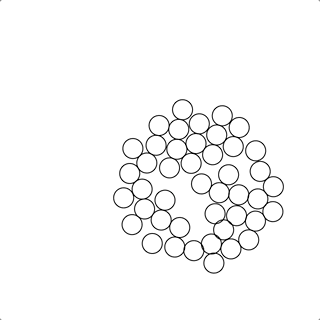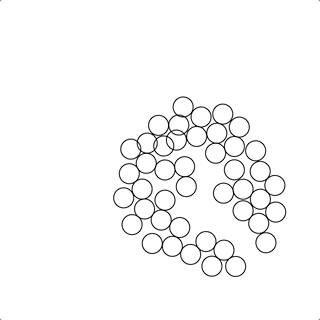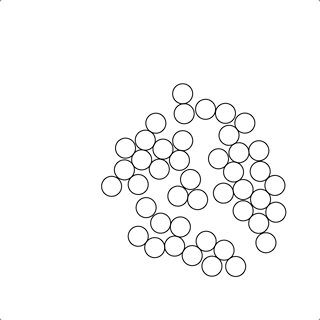
 这个方法的确可以很好的求解由粒子刻画的的无边界流体的运动状态;
这个方法的确可以很好的求解由粒子刻画的的无边界流体的运动状态;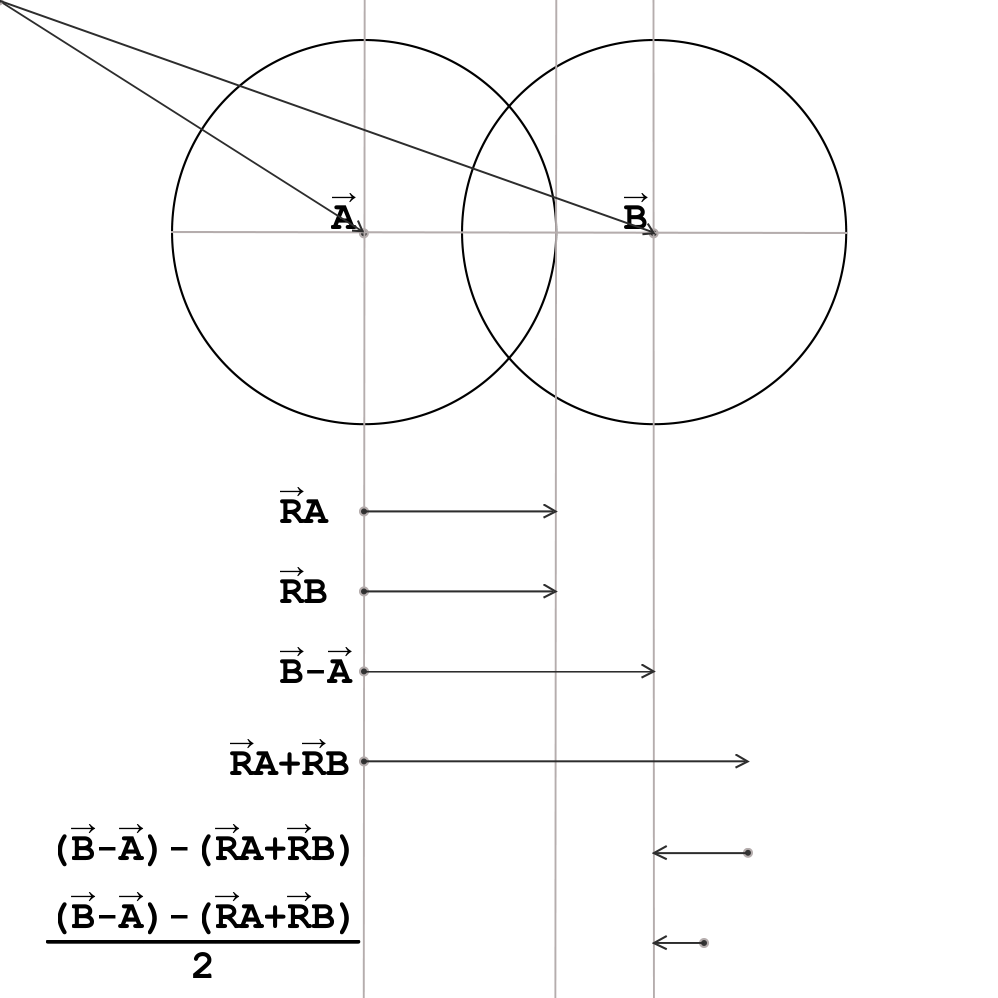
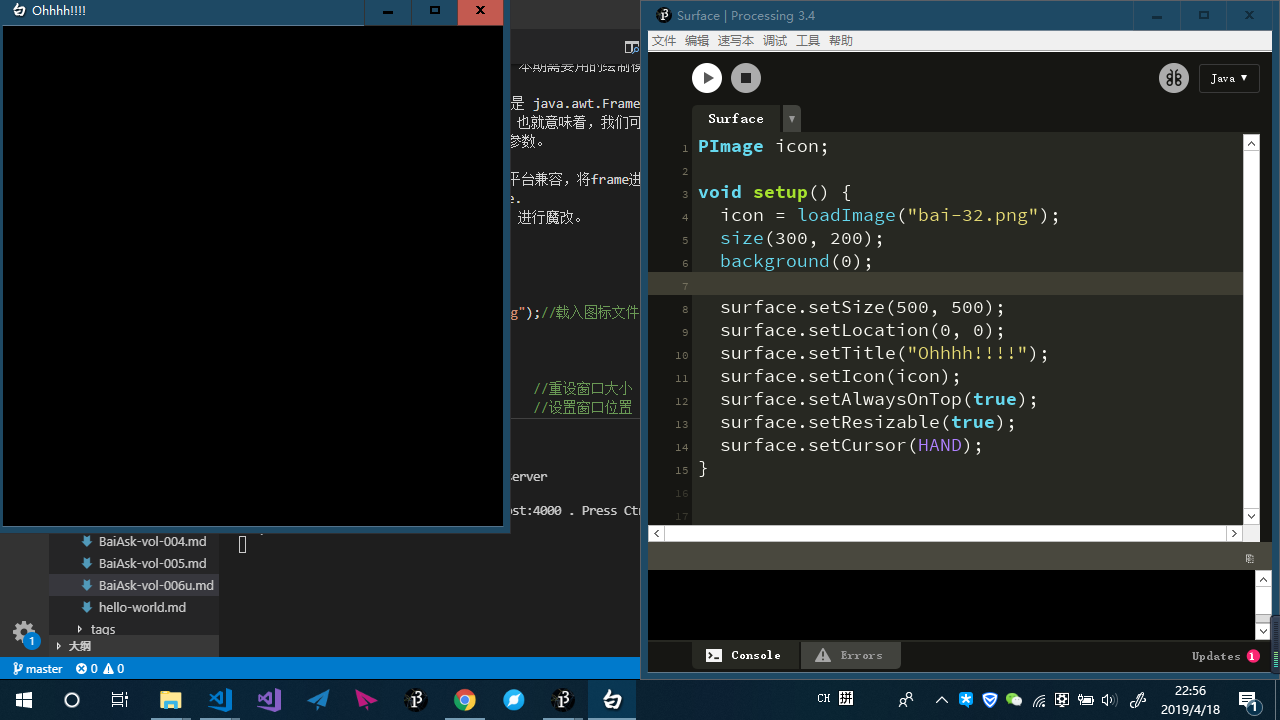 这个例子中,我们只选择了一些常用的函数进行演示,更多相关功能请参考
这个例子中,我们只选择了一些常用的函数进行演示,更多相关功能请参考  但最终运行的代码被加工成了这样:
但最终运行的代码被加工成了这样: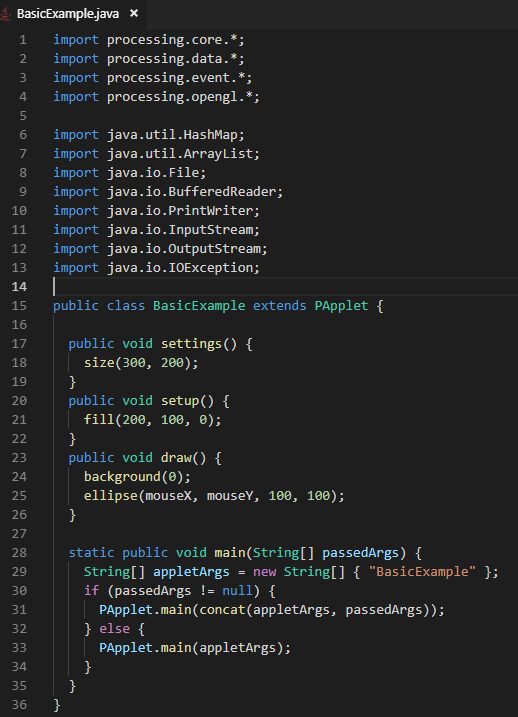

 其实Plexus的英文释义就是: n. (血管、淋巴管、神经等的)[解剖] 丛
其实Plexus的英文释义就是: n. (血管、淋巴管、神经等的)[解剖] 丛
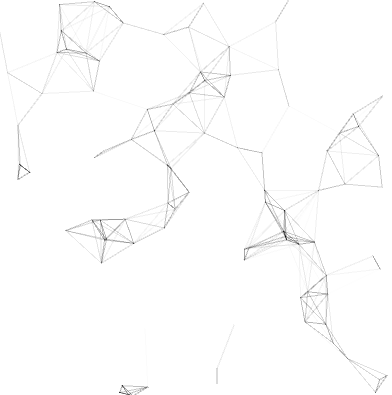

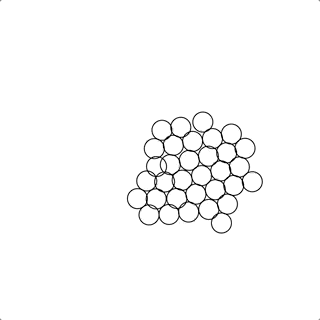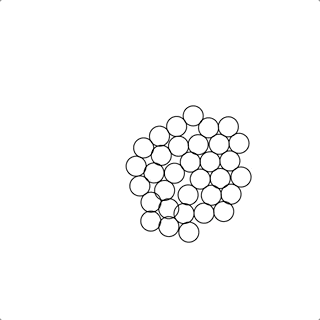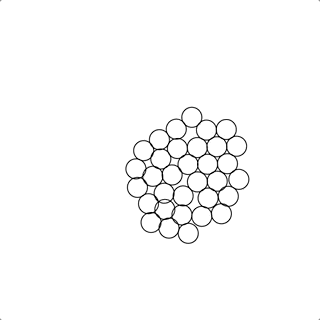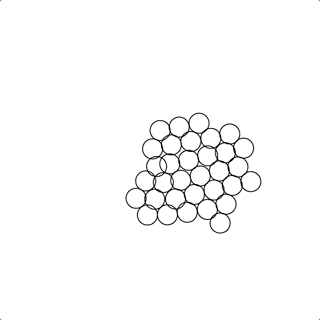
 也有时候会聚在一坨
也有时候会聚在一坨






 接下来,可以将图中的 α 角视为旋转角,可得到 α 角的对边长\(l×sinα\) 和邻边长\(l×cosα\)
接下来,可以将图中的 α 角视为旋转角,可得到 α 角的对边长\(l×sinα\) 和邻边长\(l×cosα\)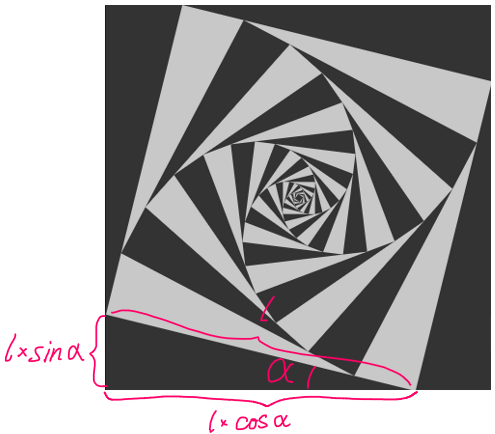 同时,另一组边的关系也可以轻易得出:$$L=(L-a)+a$$ 其中 $$(L-a)=l×cosα$$ $$a = l×sinα$$
同时,另一组边的关系也可以轻易得出:$$L=(L-a)+a$$ 其中 $$(L-a)=l×cosα$$ $$a = l×sinα$$ 那么,在得知角α的大小后,我们可以列出如下等式:$$L=l×cosα+l×sinα$$ 经变换后得到:$$L=l×(sinα+cosα)$$ $$l=\frac{L}{sinα+cosα}$$
那么,在得知角α的大小后,我们可以列出如下等式:$$L=l×cosα+l×sinα$$ 经变换后得到:$$L=l×(sinα+cosα)$$ $$l=\frac{L}{sinα+cosα}$$